Explore the data-files in the repository and familiarize with pandas¶

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Make a map that assigns the total number of memory operations per element to a given algorithm

memops = {'scal':2, 'axpby':3, 'pointwiseDot':6, 'dot':2, 'dx':3, 'dy':3,
         'arakawa':34, 'cg':42}

Now, let’s read in one of the csv files (actually they are “whitespace seperated values”) and compute the bandwidth from the time measurements, vector size and the memory operations

#read in csv file
df1 = pd.read_csv('benchmark_skl_mpi1.csv', delimiter=' ')
#add size and get rid of non-relevant columns
df1.insert(0,'size', 8*df1['n']*df1['n']*df1['Nx']*df1['Ny']/1e6)
for name, mem in memops.items():
    df1[name] = df1['size']/1000*mem/df1[name]
dfr = df1[['n','Nx','Ny','size']+list(memops.keys())]
dfr

	n	Nx	Ny	size	scal	axpby	pointwiseDot	dot	dx	dy	arakawa	cg
0	2	144	144	0.663552	314.478876	416.429966	524.460662	56.162541	97.585482	39.256309	138.435948	126.542938
1	2	288	288	2.654208	1203.520498	1272.291559	1633.536364	115.879737	183.928301	117.065735	308.217740	227.802475
2	2	384	384	4.718592	1953.722704	2088.414692	1985.410174	137.448463	198.315441	143.189693	367.836204	248.862136
3	2	576	576	10.616832	2892.511146	2698.805765	1293.980788	140.424998	207.967927	189.350724	359.265776	312.356009
4	2	768	768	18.874368	3349.488554	541.433391	595.559361	157.659528	86.322418	106.536537	290.893499	244.174862
...	...	...	...	...	...	...	...	...	...	...	...	...
315	5	576	576	66.355200	1351.859247	361.280581	246.226615	189.578161	126.820840	112.297043	147.858988	161.701097
316	5	768	768	117.964800	457.724662	231.659346	223.125189	185.692383	116.749053	103.895909	139.584366	150.029270
317	5	1152	1152	265.420800	227.990465	218.867049	207.946746	187.211376	123.177679	107.402446	141.847240	118.064374
318	5	1536	1536	471.859200	202.428668	207.751258	205.269221	104.123644	96.821422	78.527590	124.321659	133.102875
319	5	1920	1920	737.280000	144.215478	179.177603	203.338037	188.251876	123.057750	90.144151	133.416645	139.521228

320 rows × 12 columns

We want to aggregate the results with the same input parameters n, Nx, Ny

#compute mean and standard derivation of 'same' groups 
dfr=dfr.groupby(['n', 'Nx','Ny','size']).agg(['mean', 'std'])
dfr=dfr.reset_index(level=['n','Nx','Ny','size'])

#dfr['axpby']

Here, we compute the efficiency of the operations

base_bandwidth = dfr[('axpby','mean')].iloc[15] # base bandwidth at 3 2048 2048 
for name, mem in memops.items():
    dfr[(name,'eff')]= dfr[(name,'mean')]/base_bandwidth
    dfr[(name,'eff_err')]=dfr[(name,'std')]/base_bandwidth
#now display all bandwidth results

cols=[(m,'eff') for m in memops.keys()]
efficiency=dfr[['n','Nx','Ny','size']].join( dfr[cols])
cols=[(m,'eff_err') for m in memops.keys()]
efficiency=efficiency.join( dfr[cols])
#dfr=dfr.sort_values(by='size')
#efficiency=efficiency.set_index('size')

pd.set_option('precision',2)
efficiency=efficiency.sort_values(by='size')
#efficiency.loc[:,'size']
efficiency.iloc[0:20]

	n	Nx	Ny	size	scal	axpby	pointwiseDot	dot	dx	dy	arakawa	cg	scal	axpby	pointwiseDot	dot	dx	dy	arakawa	cg
					eff	eff	eff	eff	eff	eff	eff	eff	eff_err	eff_err	eff_err	eff_err	eff_err	eff_err	eff_err	eff_err
0	2	144	144	0.66	1.44	2.19	2.88	0.25	0.42	0.20	0.65	0.61	0.03	0.13	0.30	2.10e-02	7.98e-02	8.87e-03	1.38e-02	2.37e-02
8	3	144	144	1.49	3.16	5.03	6.83	0.46	0.84	0.32	0.89	0.80	0.92	0.14	0.18	6.79e-03	4.62e-02	4.47e-03	5.07e-03	5.07e-03
1	2	288	288	2.65	5.53	6.70	7.77	0.57	0.85	0.54	1.42	1.10	0.06	0.46	0.20	2.50e-02	3.30e-02	6.81e-03	1.07e-02	4.95e-02
16	4	144	144	2.65	5.54	6.52	7.69	0.55	0.65	0.33	0.92	0.76	0.09	1.10	0.23	5.95e-02	2.42e-02	1.88e-03	1.11e-02	1.44e-02
24	5	144	144	4.15	7.59	10.87	11.24	0.66	0.63	0.32	0.80	0.74	0.13	0.12	0.18	2.57e-02	2.75e-02	1.67e-03	3.84e-03	5.63e-03
2	2	384	384	4.72	8.84	9.51	9.19	0.69	0.91	0.65	1.68	1.22	0.20	0.27	0.34	3.64e-02	1.66e-02	3.16e-03	1.32e-02	5.82e-02
9	3	288	288	5.97	9.92	10.17	9.73	0.70	0.80	0.55	1.31	1.05	0.15	0.49	0.49	2.35e-02	1.94e-02	3.11e-03	1.32e-02	1.95e-02
3	2	576	576	10.62	12.80	11.92	5.94	0.67	0.94	0.85	1.68	1.45	0.67	0.50	0.97	2.72e-02	2.48e-02	1.43e-02	2.77e-02	2.66e-02
17	4	288	288	10.62	12.91	12.25	6.06	0.68	0.73	0.49	1.07	1.06	0.18	0.42	0.82	4.33e-02	1.08e-02	2.67e-03	1.05e-02	8.21e-02
10	3	384	384	10.62	12.97	12.24	6.05	0.69	0.81	0.61	1.29	1.26	0.21	0.38	0.89	2.34e-02	2.23e-02	4.82e-03	2.20e-02	1.81e-02
25	5	288	288	16.59	14.86	12.29	3.21	0.78	0.60	0.44	0.81	0.86	0.10	3.22	0.38	2.44e-02	1.00e-02	5.58e-03	2.16e-02	2.40e-02
4	2	768	768	18.87	15.10	2.47	2.98	0.79	0.40	0.72	1.31	1.13	0.44	0.04	0.16	5.68e-02	2.80e-03	8.21e-02	3.37e-02	1.56e-02
18	4	384	384	18.87	15.20	2.50	2.90	0.81	0.34	0.41	0.83	0.86	0.22	0.02	0.23	3.00e-02	5.37e-04	2.38e-03	3.18e-02	6.27e-03
11	3	576	576	23.89	16.12	9.12	2.49	0.81	0.85	0.72	0.97	1.01	0.15	2.96	0.11	4.68e-02	5.69e-03	2.78e-03	6.91e-03	1.43e-02
26	5	384	384	29.49	12.76	4.82	1.72	0.81	0.59	0.50	0.68	0.78	2.41	1.14	0.07	3.91e-02	7.62e-03	3.21e-02	5.89e-03	1.13e-02
12	3	768	768	42.47	9.24	3.37	1.26	0.85	0.80	0.71	0.87	0.94	1.07	0.66	0.03	4.37e-02	1.70e-02	1.15e-02	7.37e-03	6.82e-03
19	4	576	576	42.47	8.93	3.69	1.27	0.85	0.72	0.60	0.77	0.84	1.83	0.37	0.02	4.74e-02	9.94e-03	1.09e-02	7.72e-03	6.55e-03
5	2	1152	1152	42.47	8.01	3.92	1.25	0.83	0.97	0.92	0.97	1.04	2.78	0.31	0.03	8.50e-02	1.50e-02	5.11e-03	1.33e-02	5.36e-03
27	5	576	576	66.36	4.64	1.99	1.11	0.83	0.58	0.51	0.67	0.73	1.37	0.14	0.02	2.51e-02	2.74e-03	3.78e-03	4.70e-03	3.24e-03
6	2	1536	1536	75.50	5.02	1.62	1.07	0.80	0.88	0.86	0.86	0.92	0.63	0.10	0.02	4.04e-02	1.89e-02	3.70e-02	2.64e-02	1.29e-02

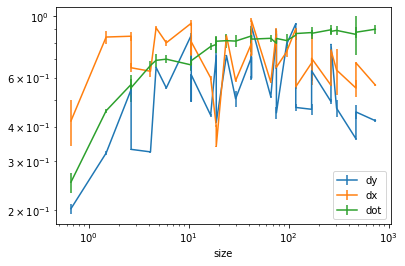
Let us try and make our first plot

fig=plt.figure()
#print(efficiency)
toPlot=efficiency['dy'].join(efficiency['size'])
ax = toPlot.plot(style='ro',x='size',y='eff',yerr='eff_err')
toPlot=efficiency['dx'].join(efficiency['size'])
ax = toPlot.plot(style='ro',x='size',y='eff',yerr='eff_err',ax=ax)
toPlot=efficiency['dot'].join(efficiency['size'])
ax = toPlot.plot(style='ro',x='size',y='eff',yerr='eff_err',ax=ax)
plt.xscale('log')
plt.yscale('log')
ax.legend(['dy','dx','dot'])

<matplotlib.legend.Legend at 0x7fd20f30d7f0>

<Figure size 432x288 with 0 Axes>

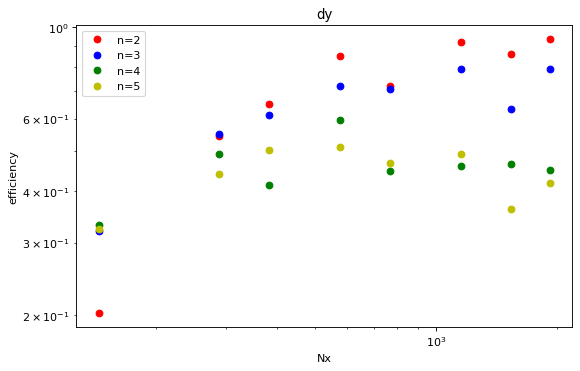
fig,ax=plt.subplots(1,1,figsize=(8,5),dpi= 80, facecolor='w', edgecolor='k')
plotlist = [('dy','eff')]
stylelist = ['ro','bo','go','yo']
#efficiency.iloc[8:24].plot(x=('size',''),y=[('cg','eff'),('arakawa','eff')],style=['ro','bo'],logx=True)
efficiency[efficiency['n']==2].plot(ax=ax, x=('Nx',''),y=plotlist,style=stylelist[0])
efficiency[efficiency['n']==3].plot(ax=ax, x=('Nx',''),y=plotlist,style=stylelist[1])
efficiency[efficiency['n']==4].plot(ax=ax, x=('Nx',''),y=plotlist,style=stylelist[2])
efficiency[efficiency['n']==5].plot(ax=ax, x=('Nx',''),y=plotlist,style=stylelist[3])
#plt.loglog()
plt.title(plotlist[0][0])
plt.xscale('log')
plt.yscale('log')
plt.ylabel('efficiency')
plt.xlabel('Nx')
plt.legend(['n=2','n=3','n=4','n=5'])
plt.show()
#base_bandwidth

A performance study of Feltor

Explore the data-files in the repository and familiarize with pandas

Explore the data-files in the repository and familiarize with pandas¶