Analysis of the dx and dy routines
Contents
Analysis of the dx and dy routines¶
import numpy as np
from collections import OrderedDict as odict
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
As done previously, we list the files we want to analyse and setup the plots
#(hardware name, number of nodes, plotstyle)
filesCPUs = {
'skl_mpi1':('skl',1), 'skl_mpi2':('skl',2), 'skl_mpi4':('skl',4), 'skl_mpi8':('skl',8),
'xeon':('xeon',1)
}
filesGPUs = {
#'p100nv_mpi1':('p100',1),
#'p100nv_mpi2':('p100',2),
'p100nv_mpi4':('p100',1), # There are 4 GPUs on one node
'p100nv_mpi8':('p100',2),
'p100nv_mpi16':('p100',4),
#'v100nv_mpi1':('v100',1),
#'v100nv_mpi2':('v100',2),
'v100nv_mpi4':('v100',1),
'v100nv_mpi8':('v100',2),
'v100nv_mpi16':('v100',4),
#'knl_mpi1':('knl',1), 'knl_mpi2':('knl',2), 'knl_mpi4':('knl',4), 'knl_mpi8':('knl',8),
'titanxp':('titanxp',1,)
}
# order by number of nodes to make labeling easier further down
cpuFiles = odict(sorted(filesCPUs.items(), key= lambda t : t[1][1]))
gpuFiles = odict(sorted(filesGPUs.items(), key= lambda t : t[1][1]))
# count number of 1 nodes in dict
number=0
for k,v in cpuFiles.items():
if v[1]==1: number+=1
arch = {'knl':(cm.Greens,450,0.5,0.33),'skl':(cm.Greys,200,0.5,0.75),'p100':(cm.Blues,550,0.5,0.43),
'v100':(cm.Purples,850,0.5,0.85),'xeon':(cm.Wistia,30,0.5,0.79),'titanxp':(cm.Oranges,155,0.5,0.70)}
intens={1:0.8, 2:0.7, 4:0.6, 8:0.5,16:0.4}
marker={2:'d', 3:'o', 4:'s',5:'p'}
Note that we compute the average bandwidth between the x and y derivative in ‘dxdy’
ns=[3]
for filelist in [gpuFiles, cpuFiles]:
for q in ['dxdy','dz','ds']:
fig,ax=plt.subplots(1,1,figsize=(6,3.7),dpi= 80, facecolor='w', edgecolor='k')
for f, v in filelist.items():
#read in csv file
df=pd.read_csv('benchmark_'+f+'.csv', delimiter=' ')
#add size and get rid of non-relevant columns
df.insert(0,'size', 8*df['n']*df['n']*df['Nx']*df['Ny']*df['Nz']/1e6/v[1])
bw = df[['n','Nx','Ny','Nz','size']]
bw = bw.assign(dx = df['size']/1000*3/df['dx'])#/arch[v[0]][1])
bw = bw.assign(dy = df['size']/1000*3/df['dy'])#/arch[v[0]][1])
bw = bw.assign(dz = df['size']/1000*3/df['dz'])
bw = bw.assign(ds = df['size']/1000*83/df['ds'])
bw = bw.assign(dxdy = 2*3*df['size']/1000/(df['dx']+df['dy']))
bw = bw.assign(dxdydz = 3*3*df['size']/1000/(df['dx']+df['dy']+df['dz']))
#compute mean and standard derivation of 'same' groups
bw=bw.groupby(['n', 'Nx','Ny','Nz','size']).agg(['mean', 'std'])
bw=bw.reset_index(level=['Nx','Ny','Nz','size'])
for n in ns:
bwn = bw.loc[n]
bwn.reset_index(inplace=True)
toPlot = bwn[q].join(bwn['size'])
#print(toPlot)
toPlot.plot(ax=ax,color=arch[v[0]][0](intens[v[1]]), marker=marker[n],ls='',markeredgecolor='k',
x='size',y='mean',label=v[0], markersize=8)
plt.xlabel('array size [MB] / # of nodes')
plt.ylabel('throughput [GB/s] / # of nodes')
plt.xscale('log')
plt.yscale('log')
plt.ylim(1e1,1e4)
#for k,v in arch.items():
# if q=='mixed' :
# plt.axhline(y=v[3],xmin=v[2],xmax=1,color=v[0](1.0),lw=2)
handles, labels = plt.gca().get_legend_handles_labels()
#handles = handles[0:len(ns)*number:len(ns)]
#labels = labels[0:len(ns)*number:len(ns)]
labels = labels[0:len(ns)]
handles = handles[0:len(ns)]
plt.legend(handles, labels, numpoints=1,loc='upper left',
fontsize='medium',framealpha=0.5)
plt.title(q)
plt.xlim(1,1000)
#if filelist == cpuFiles :
# plt.savefig(q+'_cpu.pdf',bbox_inches='tight')
if filelist == gpuFiles :
plt.legend(handles, labels, numpoints=1,loc='lower right',
fontsize='medium',framealpha=0.5)
plt.savefig(q+'_gpu.pdf',bbox_inches='tight')
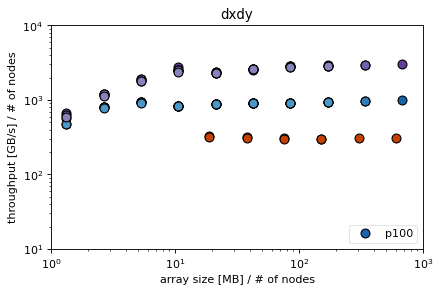
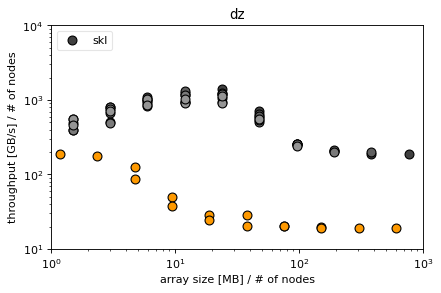
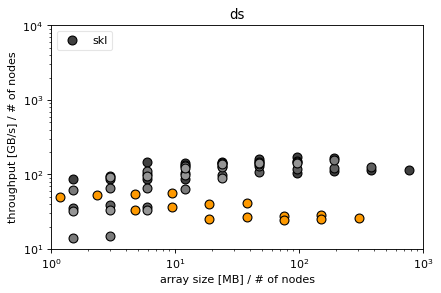
Conclusions¶
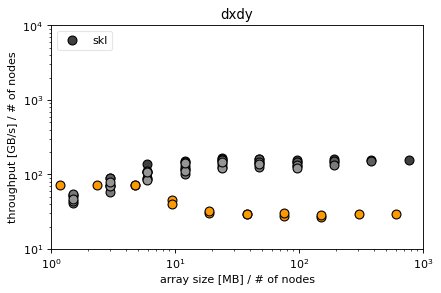
efficiency of derivatives difficult to determine for skl and knl
depends on n (the number of polynomial coefficients)
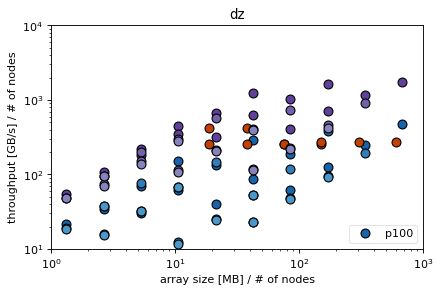
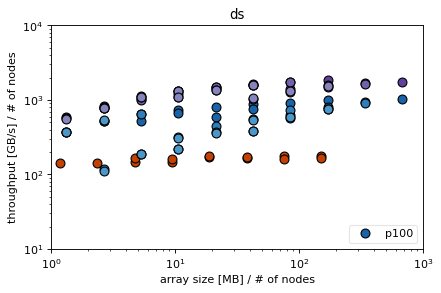
parallelizing z incurs a high latency in dz for knl and skl (probably due to high amount of memory that needs to be sent) that shows due to low computational load, ds hides the latency better for both skl and knl due to more computational load in the xy directions (communication to computation ratio small in ds but high in dz)
not parallelizing z on skl makes simple derivatives (especially dz) very fast
parallelizing xy incurs a very high latency in ds for knl, not so much for skl
for KNL the latencies in MPI seem very high in general, in fact MPI seems to be systematically slower than non-MPI also for larger sizes -> is this because MPI does not transfer MCDRAM -> MCDRAM instead copying to DDR4 RAM which is systematically slower than the MCDRAM? (Or is it because the MPI_Send calls are serialized and thus do not profit from the OpenMP parallelism?)