Contents

A test of the performance prediction model

A test of the performance prediction model

import numpy as np
from collections import OrderedDict as odict
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm

#(hardware name, number of nodes)
files = odict({})
files['i5'] = ('i5',1)
files['gtx1060'] = ('gtx1060',1)
files['skl_mpi1'] = ('skl',1)
files['skl_mpi2'] = ('skl',2)
files['skl_mpi4'] = ('skl',4)
files['knl_mpi1'] = ('knl',1)
files['knl_mpi2'] = ('knl',2)
files['knl_mpi4'] = ('knl',4)
files['p100nv_mpi1'] = ('p100',1)
files['p100nv_mpi2'] = ('p100',2)
files['p100nv_mpi4'] = ('p100',4)
files['v100nv_mpi1'] = ('v100',1)
files['v100nv_mpi2'] = ('v100',2)
files['v100nv_mpi4'] = ('v100',4)
# order by number of nodes to make labeling easier further down
files=odict(sorted(files.items(), key= lambda t : t[1][1]))
# count number of 1 nodes in dict
number=0
for k,v in files.items(): 
    if v[1]==1: number+=1
#setup plotting specifications
arch = {'knl':(cm.Greens, 450,0.5,0.33),'skl':(cm.Greys,200,0.5,0.75),   'p100':(cm.Blues,  550,0.5,0.43),
       'v100':(cm.Purples,850,0.5,0.85), 'i5':(cm.Wistia,30,0.5,0.79),'gtx1060':(cm.Oranges,155,0.5,0.70)}
intens={1:0.8, 2:0.6, 4:0.4}

Here, we setup the prediction model by giving the number of function calls and memory operations of each of the three types of primitive functions axpby, dot and dxdy

#(axpby,dot,dxdy)
latencies = odict()
latencies['scal'] = (1,0,0)
latencies['axpby'] = (1,0,0)
latencies['pointwiseDot'] = (1,0,0)
latencies['dot'] = (0,1,0)
latencies['dx'] = (0,0,1)
latencies['dy'] = (0,0,1)
latencies['arakawa'] = (3,0,6) # N = 9
latencies['cg'] = (6,2,6) # N = 13
latencies['avg']= (9,2,12) # N=23
memops = odict()
memops['scal']= (2,0,0)
memops['axpby']= (3,0,0)
memops['pointwiseDot']= (6,0,0)
memops['dot']= (0,2,0)
memops['dx']= (0,0,3)
memops['dy']= (0,0,3)
memops['arakawa'] = (16,0,18) # M = 34 -> M/N = 3.78
memops['cg'] = (20,4,18) # M = 42 -> M/N = 3.23
memops['avg'] = (36,4,36) # M = 76 -> M/N = 3.30

Let us read in the previously measured bandwidths and latencies

theo = pd.read_csv('performance.csv',delimiter=' ')
theo.set_index('arch',inplace=True)
theo.index.name = None
pd.set_option('display.float_format', lambda x: '%.2f' % x)
theo
axpby_bw axpby_bw_err dot_bw dot_bw_err dxdy2_bw dxdy2_bw_err dxdy3_bw dxdy3_bw_err dxdy4_bw dxdy4_bw_err ... axpby_lat_dist axpby_lat_dist_err dot_lat_shared dot_lat_shared_err dot_lat_dist dot_lat_dist_err dxdy_lat_shared dxdy_lat_shared_err dxdy_lat_dist dxdy_lat_dist_err
i5 29.99 0.19 9.31 0.04 27.79 2.97 29.12 2.84 25.58 1.49 ... NaN NaN 4.76 0.23 NaN NaN 0.00 1.44 NaN NaN
gtx1060 157.05 0.06 26.50 0.10 130.63 0.40 111.23 1.11 83.82 13.83 ... NaN NaN 92.06 8.70 NaN NaN 0.00 0.82 NaN NaN
skl 206.71 5.87 192.05 18.31 181.56 35.38 161.75 13.00 118.06 18.39 ... 0.00 0.26 17.28 2.32 37.93 4.14 22.70 2.11 28.52 2.10
knl 393.15 22.19 141.36 6.63 239.04 17.02 172.69 26.80 126.04 18.59 ... 9.16 0.09 54.83 1.79 119.59 5.14 9.93 0.70 52.67 3.72
p100 550.51 1.23 375.61 1.94 293.25 7.11 238.99 12.63 208.44 7.05 ... 0.00 0.27 50.89 7.06 51.67 0.59 26.23 0.05 54.40 0.35
titanXp 431.24 3.45 61.37 0.12 372.85 4.16 308.92 9.47 246.73 7.92 ... NaN NaN 44.37 5.15 NaN NaN 2.38 0.57 NaN NaN
v100 846.42 0.95 610.15 5.99 794.43 20.52 735.42 33.02 696.49 15.14 ... 0.00 0.31 88.49 4.68 97.58 0.79 4.20 0.02 37.19 0.42

7 rows × 24 columns

#define conversion function 
def toString(x): 
    if pd.isnull(x) : return 'n/a'
    #string = '%.1f'% x
    string = '%d' %np.ceil(x)
    #if np.ceil(x)<100 : string = '0'+string
    if np.ceil(x)<10 : string = '0'+string
    return string

In the followin cell we construct a table that shows the average bandwiths and latencies among a typical selection of primitive algorithms.

lines=[]
#now compute and plot the prediction 
archs = ['i5','gtx1060','skl','knl','titanXp','p100','v100']
for k in archs : 
    line =[]
    for q,l in latencies.items():
        m = memops[q]
        M = m[0]+m[1]+m[2]
        for n in [2,3,4,5]:
            bw = [theo.loc[k,'axpby_bw'],theo.loc[k,'dot_bw'],theo.loc[k,'dxdy'+str(n)+'_bw']]
            err_bw = [theo.loc[k,'axpby_bw_err'],theo.loc[k,'dot_bw_err'],theo.loc[k,'dxdy'+str(n)+'_bw_err']]
            bandwidth = M/(m[0]/bw[0] + m[1]/bw[1] + m[2]/bw[2])
            err_bandwidth = bandwidth/(m[0]/bw[0] + m[1]/bw[1] + m[2]/bw[2])*np.sqrt(
                (m[0]/bw[0]**2*err_bw[0])**2 + (m[1]/bw[1]**2*err_bw[1])**2 + (m[2]/bw[2]**2*err_bw[2])**2  )
            line.append( toString( bandwidth)+" $\pm$ "+toString(err_bandwidth))
        L = l[0]+l[1]+l[2]
        for dist in ['shared','dist']:
            lat = [theo.loc[k,'axpby_lat_'+dist], theo.loc[k,'dot_lat_'+dist], theo.loc[k,'dxdy_lat_'+dist]]
            err_lat = [theo.loc[k,'axpby_lat_'+dist+'_err'], theo.loc[k,'dot_lat_'+dist+'_err'], theo.loc[k,'dxdy_lat_'+dist+'_err']]
            latency = ( l[0]*lat[0]+ l[1]* lat[1] + l[2]*lat[2])/L #in us
            err_latency = np.sqrt( (l[0]*err_lat[0])**2 + (l[1]*err_lat[1])**2 + (l[2]*err_lat[2])**2 )/L
            if (dist == 'dist') and ((k == 'i5') or (k=='gtx1060') or (k=='titanXp')):
                line.append(toString( None))
            else: line.append(toString( latency)+" $\pm$ "+toString(err_latency))
        #print(q,latency)

    lines.append(line)
index = archs
tuples=[]  
for p in latencies.keys():
    for q in ['B(P=2) [GB/s]','B(P=3) [GB/s]','B(P=4) [GB/s]','B(P=5) [GB/s]',
              '$T_{lat}(1)$ [$\mu$s]','$T_{lat}(4)$ [$\mu$s]']:
        tuples.append((p,q))
    

cols=pd.MultiIndex.from_tuples(tuples)

avg = pd.DataFrame(lines, index=index, columns=cols)
#avg.sort_values(by=('avg','B(P=2) [GB/s]'), inplace=True)
#avg.loc[:,('cg','size')]=(avg['cg']['P=3']/1e3*9/34
#                              )*avg['cg']['lat 4 [$\mu$s]']
pd.set_option('display.float_format', lambda x: '%.0f' % x)
#avg.loc['i5',('avg','$T_{lat}(4)$ [$\mu$s]')]='n/a'
#avg.loc['gtx1060',('avg','$T_{lat}(4)$ [$\mu$s]')]='n/a'
filename='avg.tex'
with open(filename, 'wb') as f:
    f.write(bytes(avg['avg'].to_latex(
        escape=False,column_format='lp{1.5cm}p{1.5cm}p{1.5cm}p{1.5cm}p{1.2cm}p{1.2cm}',
                               bold_rows=True),'UTF-8'))
avg['avg']
B(P=2) [GB/s] B(P=3) [GB/s] B(P=4) [GB/s] B(P=5) [GB/s] $T_{lat}(1)$ [$\mu$s] $T_{lat}(4)$ [$\mu$s]
i5 26 $\pm$ 02 27 $\pm$ 02 26 $\pm$ 01 23 $\pm$ 02 01 $\pm$ 01 n/a
gtx1060 116 $\pm$ 01 108 $\pm$ 01 94 $\pm$ 09 85 $\pm$ 12 09 $\pm$ 01 n/a
skl 194 $\pm$ 20 183 $\pm$ 09 153 $\pm$ 15 147 $\pm$ 07 14 $\pm$ 02 19 $\pm$ 02
knl 281 $\pm$ 13 232 $\pm$ 24 188 $\pm$ 20 160 $\pm$ 18 13 $\pm$ 01 42 $\pm$ 02
titanXp 310 $\pm$ 02 287 $\pm$ 04 259 $\pm$ 05 230 $\pm$ 21 06 $\pm$ 01 n/a
p100 383 $\pm$ 06 336 $\pm$ 12 306 $\pm$ 08 267 $\pm$ 21 22 $\pm$ 01 33 $\pm$ 01
v100 806 $\pm$ 11 776 $\pm$ 18 755 $\pm$ 09 691 $\pm$ 43 11 $\pm$ 01 28 $\pm$ 01

In the following we compare the predicted with the measured values for the Arakawa and CG algorithm

#now compute and plot the prediction 
del latencies['avg']
del memops['avg']
for n in ['arakawa','cg'] :#latencies.keys():
    fig,ax=plt.subplots(1,1,figsize=(6,3.7),dpi= 80, facecolor='w', edgecolor='k')
    xs = np.array([0.1,1000])
    ys = np.array([1.0,1.0])
    for frac in [1.0,4/3,8/4]:
        plt.plot(xs,frac*ys,ls='--',color=cm.Greys(0.8/frac))
        plt.plot(xs,1/frac*ys,ls='--',color=cm.Greys(0.8/frac))
        
    for f, v in files.items() :#{'knl_mpi2':('knl',2)}.items():
        df=pd.read_csv('benchmark_'+f+'.csv', delimiter=' ')
        #add size and get rid of non-relevant columns
        df.insert(0,'size', 8*df['n']*df['n']*df['Nx']*df['Ny']/1e6/v[1])
        dfr = df[['n','Nx','Ny','size']+list(memops.keys())]
        #compute mean and standard derivation of 'same' groups 
        dfr=dfr.groupby(['n', 'Nx','Ny','size']).mean()
        dfr=dfr.reset_index(level=['n','Nx','Ny','size'])

        dfr['FirstLevel']='measured'
        dfr.columns=pd.MultiIndex.from_product([dfr.columns,['measured']])
        del dfr['FirstLevel']
        
        dfr['dxdy_bw'] = dfr.apply( 
            lambda row: theo.loc[v[0],'dxdy'+str(row['n','measured'].astype(int))+'_bw'], axis=1)

        dxdystring = 'dxdy_lat_shared'
        dotstring = 'dot_lat_shared'
        if v[1] > 1 : 
            dxdystring = 'dxdy_lat_dist'
            dotstrint = 'dot_lat_dist'
        for q,l in latencies.items():
            m = memops[q]
            dfr.loc[:,(q,'predicted')] = (
                                    ( l[0]*theo.loc[v[0],'axpby_lat_shared']+
                                      l[1]*theo.loc[v[0],dotstring] +
                                      l[2]*theo.loc[v[0],dxdystring]
                                    )*1e-6+
                                    (m[0]/theo.loc[v[0],'axpby_bw'] + m[1]/theo.loc[v[0],'dot_bw'] + m[2]/dfr['dxdy_bw',''])
                                       *dfr[('size','measured')]/1000)
            dfr.loc[:,(q,'meas/pred')]=dfr[(q,'measured')]/dfr[(q,'predicted')]

        toPlot = dfr[n].join(dfr[('size')],rsuffix='_size')
        toPlot.plot(kind='scatter',ax=ax,color=arch[v[0]][0](intens[v[1]]),edgecolors='k',
                     x='measured_size', y='meas/pred',label=v[0],s=64)
    handles, labels = plt.gca().get_legend_handles_labels()
    handles = handles[0:number]; labels = labels[0:number]

    #plt.plot(xs,ys)

    
    plt.legend(handles, labels, loc='upper right',ncol=2,
               scatterpoints=1,fontsize='medium',framealpha=0.5)
    plt.xscale('log')
    plt.xlim(xs[0],xs[1])
    #plt.xlabel('measured time in s')
    plt.xlabel('array size [MB] / # of nodes')
    plt.ylabel('measured / predicted time')
    plt.yscale('log', subsy=[0])#log scale, turn minor ticks off
    plt.ylim(1/3,3)
    plt.yticks([1/3,0.5,0.75,1,1.33,2,3],['1/3','1/2','3/4',1,'4/3',2,3])
    #plt.title(n)
    plt.savefig(n+'.pdf',bbox_inches='tight')

/tmp/ipykernel_11025/1666577502.py:60: MatplotlibDeprecationWarning: The 'subsy' parameter of __init__() has been renamed 'subs' since Matplotlib 3.3; support for the old name will be dropped two minor releases later.
  plt.yscale('log', subsy=[0])#log scale, turn minor ticks off

/tmp/ipykernel_11025/1666577502.py:60: MatplotlibDeprecationWarning: The 'subsy' parameter of __init__() has been renamed 'subs' since Matplotlib 3.3; support for the old name will be dropped two minor releases later.
  plt.yscale('log', subsy=[0])#log scale, turn minor ticks off
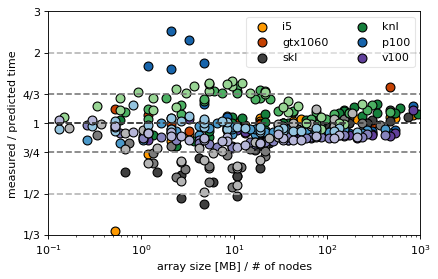
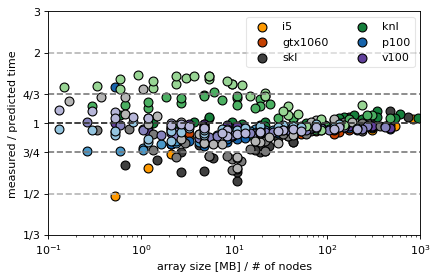
_images/5-prediction_11_2.png _images/5-prediction_11_3.png

Observations

  • plots show deviations from the predicted timing

  • the goal of the discussion is to prove that the time formula is correct because then performance can be discussed analytically and makes “scaling” plots somewhat obsolete

  • there seems to be a systematic overestimation of the knl MPI scaling (is this the fault of the implemenation? What is wrong there?)

  • skl and i5 for small sizes are mostly faster than predicted because cache effects are not included in the model

  • there seems to a drop in efficiency in GPUs when the problem size nears the full size of the GPU memory (last single node points in GTX, P100 and V100)

previous

Determine the latencies and bandwidths quantitatively

next

Details on the hardware used to gather the performance data